(C11 - GCC8.1.0)

基本属性: 信息机密性, 信息真实性, 数据完整性, 行为不可否认性.

体制: $(M,C,K_1,K_2,E,D)$ 明文空间, 密文空间, 加密密钥空间, 解密密钥空间, 加密空间, 解密空间; 加密变换 $c=E_{k_1}(m)$, 解密变换 $m=D_{k_2}(c)$.

类别: 对称加密, 非对称加密, Hash函数, 密码协议.

分析: 唯密文攻击, 已知明文攻击, 选择明文攻击, 选择密文攻击, 自适应选择明文攻击, 选择密钥攻击.

评价: 无条件安全 $P(M|C)=P(M)$; 可证明安全(破解本质为数学难题); 计算安全(破解代价超过信息价值;破解时间超过信息时效).

攻击: 被动攻击(监听-信息机密性); 主动攻击(伪造-信息真实性,篡改-数据完整性,否认-行为不可否认性).

数学基础

整除

性质: $c|a$, $c|b \Longrightarrow$ $c|ax+by$, $\forall x,y\in\mathbb{Z}$.
最大公因数: ${\rm gcd}(a,b)=\inf_{\geq 0}\{sa+tb|s,t\in\mathbb{Z}\}$.

辗转相除求${\rm gcd}$: $$\begin{align} &a=q_1b+r_1\\ &b=q_2r_1+r_2\\ &…\\ &r_{n-2}=q_nr_{n-1}+r_n \end{align}$$ 当 $r_n=0$ 时, 有 $r_{n-1}={\rm gcd}(a,b)$.

对序列中被除数与除数从$1$开始编号, 进而有递归: $$\begin{align} &a_i=(a_i/b_i)b_i+(a_i\%b_i)\\ &a_i=b_{i-1}\\ &b_i=a_{i-1}\%b_{i-1} \end{align}$$ 并约定 ${\rm gcd}(a,0)=a$.

1
2
3

int gcd(int a, int b){
	return b==0? a : gcd(b,a%b);
}

Bezout定理: 给定 $a,b\in\mathbb{Z}$, Diophantine方程 $ax+by=m$ 有解 $\Longleftrightarrow$ ${\rm gcd}(a,b)|m$.

可仅考查 $m={\rm gcd}(a,b)$, 不然, 结果只需乘相应倍数.
在递归中, 显然有 ${\rm gcd}(a,b)={\rm gcd}(a_i,b_i)$, 即 $\exists x_i,y_i\in\mathbb{Z}$ s.t. $a_ix_i+b_iy_i=m$. $$\begin{align} m&=a_ix_i+b_iy_i\\ &=b_{i-1}x_i+(a_{i-1}\%b_{i-1})y_i\\ &=b_{i-1}x_i+[a_{i-1}-(a_{i-1}/b_{i-1})b_{i-1}]y_i\\ &=y_ia_{i-1}+[x_i-(a_{i-1}/b_{i-1})y_i]b_{i-1}\\ &=x_{i-1}a_{i-1}+y_{i-1}b_{i-1} \end{align}$$

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

int extEuclid(int a, int b, int* x, int* y){  
    if (b==0){  
        *x = 1;  
        *y = 0;  
        return a;  
    } else {  
        int tempX,tempY;  
        int gcd = extEuclid(b,a%b,&tempX,&tempY);  
        *y = tempX-(a/b)*tempY;  
        *x = tempY;  
        return gcd;  
    }  
}

而使用CPP元组写法上更优雅些:

1
2
3
4
5
6
7
8
9

tuple<int,int,int>extEuclidCpp(int a, int b){  
    if (b==0){  
        return make_tuple(a,1,0);  
    } else {  
        int x,y,gcd;  
        tie(x,y,gcd) = extEuclidCpp(b,a%b);  
        return make_tuple(gcd,y,x-(a/b)*y);  
    }  
}

定理: 素数 $p$ 及 $a,b\in\mathbb{Z}$, 若 $p|ab$ 则 $p|a$ 或 $p|b$.

设 $p\nmid a$ 且 $p\nmid b$, 则 $\exists x,y$ s.t. $xp+ya=1$, 故 $x(ab)+(by)p=b$, 有 $p|b$, 矛盾.

唯一分解: $\forall n\in\mathbb{Z}$, $n=\prod p_i^{k_i}$, $p_i$ 为不同素数, $k_i\in\mathbb{Z}_+$, 形式唯一.

同余

性质: $\forall m\in\mathbb{Z}_+$, $a\equiv b({\rm mod}\ m) \Longleftrightarrow m|a-b$.

• $a\equiv b({\rm mod}\ m)$, $c\equiv d({\rm mod}\ m) \Longrightarrow a+c\equiv b+d({\rm mod}\ m)$, $ac\equiv bd({\rm mod}\ m)$, $a^n\equiv b^n({\rm mod}\ m)$.
• $ak\equiv bk({\rm mod}\ m) \Longrightarrow a\equiv b({\rm mod}\ \frac{m}{{\rm gcd}(m,k)})$.

模 $m$ 剩余类: $\mathbb{Z}/m\mathbb{Z}$.
最小非负完全剩余系: $\mathbb{Z}_m=\{0,1…,m-1\}$, 显然 $\forall x\neq y\in\mathbb{Z}_m$ s.t. $x\not\equiv y({\rm mod}\ m)$.
既约剩余系: $\mathbb{Z}_m^*=\{a\in\mathbb{Z}_m|{\rm gcd}(a,m)=1\}$.

Euler $\varphi$ 函数:
$$m=\prod_{i=1}^r p_i^{k_i}, |\mathbb{Z}_m^*|=\varphi(m)=\prod_{i=1}^r p_i^{k_i-1}(p_i-1)=m\prod_{p|m}(1-\frac{1}{p})$$

当 $m=p$ 为素数时, 有 $\varphi(p)=p-1$; $\mathbb{Z}_p^*=\{1,2,…,p-1\}$ 为循环群, 生成元个数为$\varphi(p-1)$.

考察函数性质:
若素数 $p|n$, 则 $\varphi(pn)=p\varphi(n)$;
若素数 $p\nmid n$, 则 $\varphi(pn)=(p-1)\varphi(n)$;
若 ${\rm gcd}(m,n)=1$, 则 $\varphi(m,n)=\varphi(m)\varphi(n)$.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

    int phi[n+1], prime[n+1];
    bool isSieved[n+1];

// O(n), 每个数均只遍历一次
void phiEuler(int n){
	int count = 1;
	prime[0] = 1;
	phi[1] = 1;
	for (int i = 2; i < n; ++i){
		if (!isSieved[i]){
			prime[count++] = i;
			phi[i] = i-1;
		}
		for (int j = 1; i*prime[j] <= n; ++j){
			int comp = i*prime[j];
			isSieved[comp] = 1;
			if (i%prime[j] == 0){
				phi[comp] = prime[j]*phi[i];
				break;
			} else {
				phi[comp] = (prime[j]-1)*phi[i];
			}
		}
	}
}

定理: 若 ${\rm \gcd}(a,m)=1$, $x$ 遍历 $\mathbb{Z}_m^*$, 则 $ax$ 也遍历$\mathbb{Z}_m^*$.

考虑 ${\rm gcd}(ax,m)=1$ 及 $ax_i\not\equiv ax_j({\rm mod}\ m)$, $i\neq j$.

逆元: 若 ${\rm gcd}(a,m)=1$, 则 $\exists ! x\in\mathbb{Z}_m^*$ s.t. $ax\equiv 1({\rm mod}\ m)$.
Euler: 若 ${\rm gcd}(a,m)=1$, 则 $a^{\varphi(m)}\equiv 1({\rm mod}\ m)$.

$\mathbb{Z}_m^*=\{x_1,…,x_{\varphi(m)}\}=\{ax_1,…,a_{\varphi(m)}\}$, 故 $\prod x_i\equiv\prod ax_i({\rm mod}\ m)$, 已知 ${\rm gcd}(x_i,m)=1$, 得 $m|a^{\varphi(m)}-1$.

特别 $m=p$ 为素数时, Fermat: 若 $p\nmid a$, 则 $a^{p-1}\equiv 1({\rm mod}\ p)$, 有 $a^{-1}\equiv a^{p-2}({\rm mod}\ p)$.
由扩展Euclid, ${\rm gcd}(a,m)=1$, $\exists s,t\in\mathbb{Z}$ s.t. $as+tm=1$, 即 $a^{-1}\equiv s({\rm mod}\ m)$.

1
2
3
4
5
6
7
8
9

int inverse(int a, int m){
    int s,t;
    int gcd = extEuclid(a,m,&s,&t);
    if (gcd == 1){
        return s;
    } else {
        return 0;
    }
}

wilson: 素数 $p$ 有 $(p-1)!\equiv -1({\rm mod}\ p)$.

$\mathbb{Z}_m^*$ 中元素均存在逆, 自逆仅 $1,p-1$; $\{2,3,…,p-2\}$ 中两两配对互逆.

1
2
3
4
5
6
7

bool wilson(int p){
    int factMod = 1;  
    for (int i = p-1; i >= 1; --i){  
        factMod = (factMod*i)%p;  
    }
    return (factMod+1)%p == 0;
}

• 仿射: ${\rm gcd}(a,26)=1$, 密钥对数量 $26\varphi(26)-1=311$.
  加密 $c=E_{a,b}(m)=am+b({\rm mod}\ 26)$.
  解密 $m=D_{a,b}(c)=a^{-1}(c-b)({\rm mod}\ 26)$.

同余式

同余式 $f(x)\equiv a_nx^n+…+a_1x+a_0({\rm mod}\ m)$, $a_i\in\mathbb{z}$, $m\in\mathbb{Z}_+$.
同余方程 $f(x)\equiv 0({\rm mod}\ m)$ 至多有 $m$ 个解(剩余类).

一次同余 $ax\equiv b({\rm mod}\ m)$, $a,b\in\mathbb{Z}$, $m\in\mathbb{Z}_+$ 有解 $\iff {\rm gcd}(a,m)|b$.

$ax\equiv b({\rm mod}\ m)$ 在 ${\rm gcd}(a,m)=1$ 时有唯一解 $x\equiv a^{-1}b({\rm mod}\ m)$. 记 $d={\rm gcd}(a,m)$, 有 $\frac{a}{d}x\equiv \frac{b}{d}({\rm mod}\ \frac{m}{d})$, 即 $x=\frac{b}{d}(\frac{a}{d})^{-1}+k\frac{m}{d}$, $k\in\mathbb{Z}$. 考虑 $k=qd+r$, $q,r\in\mathbb{Z}$, $0\leq r< d$, $x=[\frac{b}{d}(\frac{a}{d})^{-1}({\rm mod}\frac{m}{d})+r\frac{m}{d}]({\rm mod\ m})$.

求解步骤:
(1) 扩展Euclid求 $d={\rm gcd}(a,m)$, 记 $sa+tm=d$;
(2) $b\%d=0$ 判断有无解;
(3) 设 $b’=b/d$, $m’=m/d$, $s’\equiv s({\rm mod}\ m’)$;
(4) 得 $x\equiv s’b’+rm’\ ({\rm mod}\ m)$, $r=0,1,…,d-1$.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

int linearCongEq (int a, int b, int m, int ansX[]){  
    a %= m;  
    b %= m;  
    int s,t;  
    int origM = m;  
    int d = extEuclid(a,m,&s,&t);  
    if (b%d == 0){  
        b /= d;  
        m /= d;  
        s %= m;  
        for (int r = 0; r <= d-1; ++r){  
        ansX[r] = ((s*b+r*m)%(origM)+origM)%origM;  
        }  
        return d;  
    } else {  
        return 0;  
    }  
}

一次同余组(CRT): $m_{i{1\leq i \leq k}}$ 两两互素, 同余组 $x\equiv a_i({\rm mod\ m_i})_{{1\leq i\leq k}}$ 有唯一解 $x=\sum M_i M_i^{-1} a_i \ ({\rm mod}\ m)$. 其中, $m=\prod m_i$, $M_i=m/m_i$, $M_i^{-1}$ 为模 $m_i$ 上的逆.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

long crt (int a[],int m[],int n){  
    int modSepM[n];  
    int modIevM[n];  
    long modM[n];  
    long prodM = 1;  
    long x = 0;  
    for (int i = 0; i < n; ++i){  
        prodM *= m[i]*1L;  
    }  
    for (int i = 0; i < n; ++i){  
        modM[i] = 1L*prodM/m[i];  
        modSepM[i] = (1L*modM[i])%m[i];  
        modIevM[i] = inverse(modSepM[i],m[i]);  
        if (!modIevM[i]){  
            return 0;  
        }  
    }  
    for (int i = 0; i < n; ++i) {  
        x = (x+1L*modIevM[i]*modM[i]*a[i])%prodM;  
    }  
    x = (x+prodM)%prodM;  
    return x;  
}

• RSA: 素数$p,q$, $n=pq$, ${\rm gcd}(e,\varphi(n))=1$, $\varphi(n)=(p-1)(q-1)$.
  公钥 $(e,n)$, 加密 $c=E_{e,n}(m)\equiv m^e({\rm mod}\ n)$.
  私钥$d\equiv e^{-1}({\rm mod}\ \varphi(n))$, 解密 $m=D_{d,n}(m)\equiv c^d({\rm mod}\ n)$.
  

快速模幂 $r\equiv t^e({\rm mod}\ n)$.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

int fastPowerMod (int t, int ex, int n){
    int r = 1; 
    while (ex){
        if (ex&1){
            r = (1LL*r*t)%modular;
        }
        t = (1LL*t*t)%modular;
        ex >>= 1;
    }
    return r;
}

二次剩余

$ax^2+bx+c\equiv 0({\rm mod}\ m)$ 总能简化为 $x^2\equiv d({\rm mod}\ q^k)$, $q$ 为素数, $a,b,c,d,m,k\in\mathbb{Z}_+$.
仅考虑 $x^2\equiv a({\rm mod}\ q)$, ${\rm gcd}(a,p)=1$, $a\in\mathbb{Z}$ 为模素数 $q$ 的二次剩余.

Euler: ${\rm gcd}(a,p)=1$, $p$ 为奇素数, $a\in\mathbb{Z}$:
模 $p$ 的二次剩余恰有 $\frac{p-1}{2}$ 个.
$a$ 为模 $p$ 二次剩余 $\iff a^{\frac{p-1}{2}}\equiv 1({\rm mod}\ p)$, 此时 $x^2\equiv a({\rm mod}\ p)$ 有二解.
$a$ 为模 $p$ 二次非剩余 $\iff a^{\frac{p-1}{2}}\equiv -1({\rm mod}\ p)$.

显然 $i^2\equiv(p-i)^2({\rm mod}\ p)$; 若 $j^2\equiv i^2({\rm mod}\ p)$, $1\leq i<j<\frac{p}{2}$, 则 $p|j-i$ 或 $p|j+i$, 但 $j+i<p$, 矛盾.

$a$ 为模 $p$ 二次剩余时, $\exists x_0\in\mathbb{Z}$, ${\rm gcd}(x_0,p)=1$, $x_0^2\equiv a({\rm mod}\ p)$, 故 $a^{\frac{p-1}{2}}\equiv x_0^{p-1}\equiv 1({\rm mod}\ p)$.

$a$ 为模 $p$ 二次非剩余时, 考虑 $a^{p-1}\equiv 1({\rm mod}\ p)$, 则 $p|{\frac{p-1}{2}}-1$ 或 $p|{\frac{p-1}{2}}+1$, 但 $x^{\frac{p-1}{2}}\equiv 1({\rm mod}\ p)$ 的全部解恰为全部的二次剩余.

Legendre: $(\frac{a}{p})=a^{\frac{p-1}{2}}\%p=1\ {\rm or}\ -1\ {\rm or}\ 0$, $p$ 为素数, $a\in\mathbb{Z}$.

$$ (\frac{1}{p}) = 1;\ (\frac{ab}{p})=(\frac{a}{p})(\frac{b}{p}); \ (\frac{a+b}{p})=(\frac{a}{p})+(\frac{b}{p})$$

$$(\frac{a^2}{p})=1,\ {\rm gcd}(a,p)=1$$

$$ (\frac{-1}{p})=\begin{cases} &1,\ &p\%4=1\\ &-1,\ &p\%4=3 \end{cases}$$

$$ (\frac{2}{p})=\begin{cases} &1,\ &p\%8=1,7\\ &-1,\ &p\%8=3,5 \end{cases}$$

二次互反: $(\frac{p}{q})(\frac{q}{p})=(-1)^{\frac{p-1}{2}\frac{q-1}{2}}$, $p\ne q$ 为奇素数.

Guass: 奇素数 $p$, $a\in\mathbb{Z}$, ${\rm gcd}(a,p)=1$, 设 $M_{a,p}=\{ka\%p, \ k=1,2,…,\frac{p-1}{2}\ |\ ka\%p>\frac{p}{2}\}$, 记 $m(a,p)=|M_{a,p}|$, 则 $(\frac{a}{p})=(-1)^{m(a,p)}$.

设 $K=\{ka\%p\ |\ k=1,2,…,\frac{p-1}{2}\}$, $b_i\in M$, $c_j\in M-K$, $i=1,2,..,m(a,p)$, $j=1,2,…,\frac{p-1}{2}-m(a,p)$.

显然有 $c_j\ne p-b_i$, $\forall i,j$; 否则 $p|b_i+c_j$, 即 $\exists x,y\in\mathbb{Z}$, $x,y<\frac{p}{2}$ s.t. $p|a(x+y)$, 但 $x+y<p$, 矛盾.

故 $a^{\frac{p-1}{2}}(\frac{p-1}{2})!\equiv\prod c_j \prod (p-b_i)\equiv (-1)^{m(a,p)}(\frac{p-1}{2})!({\rm mod}\ p)$.

Eisenstein: $a$ 为奇数时, 记$e(a,p)=\sum\lfloor\frac{ka}{p}\rfloor$, 有 $e(a,p)\equiv m(a,p)({\rm mod}\ 2)$.

不妨设 $ka=d_kp+r_k$, $0\leq r_k\leq p-1$, $d_k,r_k\in\mathbb{Z}$, 有 $p\sum d_k+\sum r_k=\sum ka = \sum c_j+\sum (p-b_i)$, 故 $\sum d_k\equiv m(a,p)({\rm mod}\ 2)$; 显然 $e(a,p)=\sum d_k$.

$q\ne p$ 为奇素数时, $\not\exists x,y\in\mathbb{Z}$, $x,y<\frac{p}{2}$ s.t. $xp=qy$, 即 $e(p,q)+e(q,p)=\frac{p-1}{2}\frac{q-1}{2}$.

$a=2$ 时, $\lfloor\frac{p}{4}\rfloor\leq k\leq \lfloor\frac{p}{2}\rfloor$, 有 $m=\lfloor\frac{p}{2}\rfloor-\lfloor\frac{p}{4}\rfloor$.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

int fastLegendre(int a, int p){
    int s;
    int e = 0;
    if (a == 0 || a == 1){
        return a;
    } else {
        while (a%2 == 0){
            a /= 2;
            ++e;
        }
        if (e%2 == 0 || p%8 == 1 || p%8 == 7){
            s = 1;
        } else {
            s = -1;
        }
        if (p%4 == 3 && a%4 == 3){
            s = -s;
        }
        if (a == 1){
            return s;
        } else {
            return s*fastLegendre(p%a,a);
        }
    }
}

• Rabin: 素数 $p\equiv q\equiv 3({\rm mod}\ 4)$.
  公钥 $n=pq$, 加密 $c\equiv E_{n}(m)\equiv m^2({\rm mod}\ n)$.
  私钥 $(p,q)$, 解密 $m\equiv D_{p,q}(c)\equiv \pm c^{\frac{p+1}{4}}({\rm mod}\ p)\equiv \pm c^{\frac{q+1}{4}}({\rm mod}\ q)\ (2\ {\rm in}\ 4)$.

原根

原根: $a,m\in\mathbb{Z}$, $m>1$, ${\rm gcd}(a,m)=1$, 记 ${\rm ord}_m(a)=\inf\{x\in\mathbb{Z}_+\ | \ a^x\equiv 1({\rm mod}\ m)\}$ 称为 $a$ 对模 $m$ 的阶; 特别, ${\rm ord}_m(a)=\varphi(m)$ 时称 $a$ 为模 $m$ 的原根.

定理: $a,m\in\mathbb{Z}$, $m>1$, ${\rm gcd}(a,m)=1$, 则 $a^n\equiv 1({\rm mod}\ m)\iff {\rm ord}_m(a)|n$. 特别, ${\rm ord}_m(a)|\varphi(m)$.

定理: $g$ 为模 $m$ 原根 $\iff g^{\frac{\varphi(m)}{p_i}}\not\equiv 1({\rm mod}\ m)$, $\forall$ 素数 $p_i|\varphi(m)$.

必要性: 显然.

充分性: 若 $\exists e<\varphi(m)$ s.t. $g^e\equiv 1({\rm mod}\ m)$; 不妨设 $\frac{\varphi(m)}{e}=kp$, $k\in\mathbb{Z}$, $p$ 为素数; 进而 $g^{\frac{\varphi(m)}{e}\equiv(g^p)^k\equiv 1({\rm mod}\ m)}$, 矛盾.

定理: $a,m,d\in\mathbb{Z}_+$, ${\rm gcd}(a,m)=1$, ${\rm ord}_m(a^d)=\frac{{\rm ord}_m(a)}{{\rm gcd}({\rm ord}_m(a),d)}$.
推论: 模 $m$ 存在原根时, 有 $\varphi(\varphi(m))$ 个原根; 同时原根为模 $m$ 上本原多项式的全部解.

以下显然:
${\rm ord}_m(a)={\rm ord}_m(a^{-1})$.
$b\equiv a({\rm mod}\ m)$, 则 ${\rm ord}_m(b)={\rm ord}_m(a)$.
${\rm gcd}(a,m)=1$, $a^0,a^1,…,a^{{\rm ord}_m(a)-1}$ 两两模 $m$ 不同余.
特别, $g$ 为模 $m$ 原根时, 恰好有 $\mathbb{Z}_p^*={g^0,g^1,…,g^{\varphi(g)-1}}$.
$g$ 为模 $m$ 原根时, $x,y\in\mathbb{Z}$, $g^x\equiv g^y({\rm mod}\ m) \iff x\equiv y({\rm mod}\ \varphi(m))$.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

bool nMod1(int a, int n, int p, int* primeFact){
    int num = 0, r;
    while(primeFact[num]){
        r = fastPowerMod(a,n/primeFact[num],p);
        if (r == 1){
            break;
        } else {
            ++num;
        }
        if(!primeFact[num]) {
            return true;
        }
    }
    return false;
}

int minPrimeRoot(int p){
    int n = p-1, res = 0;
    int primeFact[10] = {0};
    factPrime(n,primeFact);
    for (int i = 2; i <= p/2; ++i) {
        if (nMod1(i,n,p,primeFact)){
            res = i;
            break;
        }
    }
    return res;
}

• D-H协议: 大素数 $p$ 和模 $p$ 原根 $g$, 任选 $2\leq x,y\leq p-2$.
  公钥 $(p,g)$, 私钥 $x,y$.
  握手: $k_{X\to Y}\equiv g^x({\rm mod}\ p)$, $k_{Y\to X}\equiv g^y({\rm mod}\ p)$.
  密钥: $k\equiv k_{Y\to X}^x\equiv k_{X\to Y}^y \equiv g^{xy}({\rm mod}\ p)$.

• ElGamal: 大素数 $p$ 和模 $p$ 原根 $g$, 任选 $2\leq a\leq p-2$, $Y_a\equiv g^a({\rm mod}\ p)$.
  公钥 $(p,g,Y_a)$, 加密 $u\equiv g^k({\rm mod}\ p)$, $v\equiv mY_a^k({\rm mod}\ p)$, $c=E_{p,g,Y_a,k}(m)=(u,v)$, 任选 $2\leq k\leq p-2$.
  私钥 $a$, 解密 $m\equiv D_a(c)\equiv \frac{v}{u^a}({\rm mod}\ p)$.
  

群

有限群: 非空有限集 $G$ 上代数运算满足结合律, 存在单位元(记 $e$), 逆元(记 $a^{-1}$);
记 $|G|={\rm Card}(G)$ 为阶; 定义 $a^{-n}=(a^{-1})^n$, $a^0=e$.

半群: 只满足结合律.
幺半群: 存在单位元的半群.
交换半群: 满足交换律的半群.
交换幺半群: 存在单位元满足交换律的半群.
Abel群: 满足交换律的群.
消去律: 可由结合律和逆元推得.

元素的阶: $|a|=\inf \{n\in\mathbb{N}_+\ |\ a^n = e\}$ 或 $\infty$;
$|a^{-1}|=|a|$, $|a^d|=\frac{|a|}{{\rm gcd}(|a|,d)}$; 若 $n\in\mathbb{Z}$, $a^n=e$ 则 $|a||n$.

不妨设 $|a|=n$, $|a^d|=m$, 由于 $a^{dm}=e$, 即 $n|dm$, 进而 $\frac{n}{{\rm gcd}(n,d)}|\frac{d}{{\rm gcd}(n,d)}m$, 即 $\frac{n}{{\rm gcd}(n,d)}|m$.

同时 $(a^d)^{\frac{n}{{\rm gcd}(n,d)}}=e$, 即 $m|\frac{n}{{\rm gcd}(n,d)}$.

子群: 群 $G$ 的非空子集 $H$ 关于 $G$ 的代数运算构成群, 记 $H<G$; 真子群即非平凡子群({e},G);
$H<G$ 则 $e\in H$, $e\in G$, 且 $\forall a\in H$, $a^{-1}\in G$; $H<G \iff \forall a,b\in H$, $ab^{-1}\in H$.

循环群: 群 $G$ 的非空子集 $S$, 生成子群 $\langle S\rangle=\bigcap_{S\subset H<G}H=\{\prod a_i^{l_i}\ |\ a_i\in S, l_i=\pm 1\}$;
特别 $S=\{a\}$ 时, 循环子群 $\langle S\rangle=\langle a\rangle=\{a^n\ |\ n\in\mathbb{Z}\}$;
特别 $G=\langle a\rangle$ 时为循环群 $\iff\exists a\in G$ s.t. $|a|=|G|$;
循环群子群仍为循环群; 无限循环群同构于 $\mathbb{Z}$, $n$ 阶循环群同构于 $\mathbb{Z}_n$.

不妨设 $H<G=\langle a\rangle$, $H\ne {e}$, $\exists a^k\in H$, $a^{-k}\in H$, 则 $\exists r,t\in\mathbb{Z}_+$, $q\in\mathbb{Z}$ s.t. $a^r\in H$, $n=qr+t$; 进而 $a^n=a^{qr+t}\in H$ 即 $t=0$, 故 $H\subset \langle a^r\rangle$.

陪集: $H<G$, $\forall a\in G$, $aH$ 为左陪集;
$a\in G$, $aH=H\iff a,b\in G$, $aH=bH$ 或 $aH\cap bH=\empty$, $|H|=|aH|$; $G=\bigsqcup_{g\in G}gH$.

Lagrange: 记 $[G:H]=\frac{|G|}{|H|}$, $|G|=[G:H]|H|$; $|a|||G|$.

正规子群: $H<G$, $\forall a\in G$, $aH=Ha$, 记 $H\lhd G$; $H<G$, $\forall a\in G$, $H\lhd G \iff aHa^{-1}=H \iff aHa^{-1} \subset H \iff aha^{-1}\in H$, $\forall h\in H$.

商群: $H\lhd G$, $G/H=\{aH\ |\ a\in G\}$, $aH\ast bH=(ab)H$.

同态: 保持代数运算不变的映射, 双射时为同构.
群同态: 群 $G_1,G_2$, 映射 $f:G_1\to G_2$, $f(ab)=f(a)f(b)$, $\forall a,b\in G_1$.

• 同态 Paillier: 素数 $p,q$, $n=pq$, $\lambda = {\rm lcm}(p-1)(q-1)$ 最小公倍数, $g\in\mathbb{Z}_{n^2}^*$ s.t. ${\rm gcd} (\frac{g^\lambda \% n^2 -1}{n},n)=1$.
  公钥 $(n,g)$, 加密 $c\equiv E_{n,g}(m)\equiv g^m r^n({\rm mod}\ n^2)$, $r\in\mathbb{Z}_n^*$.
  私钥 $\lambda$, 解密 $m\equiv D_\lambda(c)\equiv\frac{c^\lambda \%n-1}{g^\lambda \&n-1}({\rm mod}\ n^2)$.
  加法同态: $m_1+m_2=D_\lambda[E_{n,g}(m_1)E_{n,g}(m_2)]$.

置换群: 非空集合 $X$ 上所有可逆变换(双射)关于复合构成对称群 $S_x$; $S_x$ 子群称为变换群;
特别 $|X|=n$ 时, 记 $S_x = S_n$, $S_n$及其子群称为置换群, 元素 $\sigma$ 称为置换; $|S_n|=n!$.

轮换: $f\in S_n$, $i_1,…,i_r\in X$, $f(i_1)=i_2,…,f(i_{r-1})=i_r,f(i_r)=i_1$ 且保持其他元素不变时, $f=(i_1,i_2,…,i_r)$ 称为 $r$ -轮换;
特别 $r=1$ 时为恒等变换, $r=2$ 时称为对换;
任意置换可唯一表示为不相交的轮换之积; 任意轮换可以表示为对换之积.

Cayley: 任意有限群同构于一置换群.

环和域

环: 非空集合 $R$ 上两个代数运算 $(+,\cdot)$, $(R,+)$ 为Abel群, $(R,\cdot)$ 为半群, $\cdot$ 对 $+$ 有双边分配律;
为区别, $+$ 的单位元称为零元(记 $0$), 逆元称为负元(记 $-a$).

单位: $a\in R$, $\exists b\in R$ s.t. $ab=ba=e$, 则称 $a$ 为单位; 环中所有单位构成单位群, 记 $U(R)$; $U(\mathbb{Z}_m)=\mathbb{Z}_m^*$.
零因子: 非零元 $a,b\in R$ s.t. $ab=0$, $a$ 为 $b$ 的左零因子.

交换环: $(R,\cdot)$ 为交换半群.
交换幺环: $(R,\cdot)$ 为交换幺半群.
无零因子环: $(R,\cdot)$ 为无零因子半群.
整环: $(R,\cdot)$ 为无零因子交换幺半群.
域: $(R-\{0\},\cdot)$ 为Abel群.

双边理想: 非空集合 $I\subset R$, $I$ 对 $+$ 封闭, 对 $\cdot$ 吸收, 即 $\forall s\in R$, $sI\subset I$, $Is\subset I$, 记 $I \lhd R$; $d\mathbb{Z}\lhd\mathbb{Z}$.

商环: $I\lhd R$, $R/I < R$; $R/I=\{a+I\ | \ a\in R\}$.
$(a+I)+(b+I)=(a+b)+I$, $(a+I)(b+I)=(ab)+I$.

映射: 不妨设 $a_1+I=a_2+I$, $b_1+I=b_2+I$, 则有 $(a_1b_1)+I=(a_2b_2)+I$. 考虑 $a_1-a_2\in I$, $b_1-b_2\in I$, 有 $a_1=s+a_2$, $b_1=t+b_2$, $s, t\in I$, 进而 $a_1b_1=a_2b_2+x=a_2b_2+(sb_2+ta_2+st)$, 同时 $x\in I$.

封闭: $\forall x\in I$, $(a+x)(b+x)=ab+(a+b+x)x\in (ab)+I$.

由此可知, 理想的吸收性可确保商环存在.

生成理想: 非空集合 $S\subset R$, 包含 $S$ 的所有理想的交集;
特别 $S=\{a\}$ 时, 记 $\langle S\rangle=\langle a\rangle$ 为 $a$ 生成的主理想;
特别 $R$ 为交换幺环时, 主理想 $\langle a\rangle=\{ra\ | \ r\in R\}$;
$\mathbb{Z}$ 的所有理想均为主理想.

任取非平凡理想 $I\lhd \mathbb{Z}$, $\exists$ 最小 $t\in\mathbb{Z}_+$, $\forall m\in I$, $m=qt+r$, $q,r\in I$, $0\leq r<t$, 即 $r=0$, $I=\langle t\rangle$.

素理想: 交换幺环 $R$, 非平凡 $P\lhd R$, 若 $ab\in P$, 有 $a\in P$ 或 $b\in P$; 特别整环中, 素元 $p$, $\langle p\rangle$ 为素理想.
交换幺环 $R$, $P\lhd R$, $R/P$ 为整环 $\iff P$ 为素理想.
极大理想: 交换幺环 $R$, 非平凡 $M\lhd R$, 无真包含 $M$ 的非平凡理想.
交换幺环 $R$, $M\lhd R$, $R/M$ 为域 $\iff M$ 为极大理想.
极大理想一定为素理想, 反之不然.

Euclid整环(ED): 满足Euclid性的整环, $\forall a,b\in R-\{0\}$, 有映射 $\varepsilon: R-\{0\}\to \mathbb{Z}_+$ s.t. $\varepsilon(a)\leq\varepsilon(ab)$, $\exists r,q\in R$ s.t. $a=bq+r$, $\varepsilon(r)<\varepsilon(b)$ 或 $r=0$; 其上有最大公因数.
主理想整环(PID): 理想均为主理想的整环; 其上素元和不可约元等价, 素理想和极大理想等价; 素元为非零元非单位 $p$ s.t. $a,b\in R$, 若 $p|ab$, 有 $p|a$ 或 $p|b$; 不可约元为非零元非单位 $q$ s.t. $a,b\in R$, 若 $q=ab$, 有 $a$ 或 $b$ 为单位.
唯一析因整环(UFD): 整环 $R$ 中非零元非单位的元素可以唯一表示为有限个不可约元的积.

定理: 所有域都是ED; 所有ED都是PID; 所有PID都是UFD.

特征: ${\rm char}(R)=\inf\{n\in\mathbb{Z}_+\ | \ na=a,\forall a\in R\}$ 或0; ${\rm char}(\mathbb{Z})=0$, ${\rm char}(\mathbb{Z}_m)=m$;
整环特征必为0或素数, 非空有限域特征必为素数, ${\rm char}(F_p)=p$;
$\forall a,b\in F_p$, $(a+b)^p=a^p+b^p$.

$|e| = \infty$ 时, ${\rm char}(R)=0$.

$|e| = n$ 时, 若 $n$ 为合数, $\exists p|n$，不妨设 $pc=n$, $ne=(pe)(ce)=0$, 则 $pe=0$ 或 $ce=0$, 矛盾. $\forall a\in R$, $na=(ne)a=0$.

单变量多项式环: 整环 $R$ 上整环 $R[x]=\{a_nx^n+…+a_1x+a_0\ | \ a_i\in R\}$;
记 $f(x)=a_nx^n+…+a_1x+a_0$, $a_n\ne 0$ 时, 记 ${\rm deg}f=n$; 特别 ${\rm deg}0=-\infty$.
$f(x),g(x),h(x)\in R[x]$, $f(x)g(x)=h(x)$, 则 ${\rm deg}f+{\rm deg}g={\rm deg}h$.
域 $K$, $f(x)\in K[x]$, ${\rm deg}f>0$, $p(x)$ 为 $f(x)$ 次数最小的因式, 则 $p(x)$ 为 $K[x]$ 上不可约多项式, 且 ${\rm deg}p\leq \frac{1}{2}{\rm deg}f$.

带余除法: $f(x),g(x)\in R[x]$, 则 $\exists q(x),r(x)\in R[x]$ s.t. $f(x)=q(x)g(x)+r(x)$, ${\rm deg}r<{\rm deg}g$.
$f(x)\in R[x]$, $a\in R$, 则 $\exists q(x)$ s.t. $f(x)=(x-a)q(x)+f(a)$.
$f(x)\in R[x]$, $a\in R$, 则 $x-a|f(x)\iff f(a)=0$.
同余: 首一多项式 $m(x)\in R[x]$, $f(x),g(x)\in R[x]$, $m(x)|f(x)-g(x)$, 记 $f(x)\equiv g(x)({\rm mod}\ m(x))$.

Euclid: 域 $K$ 上 $K[x]$ 为ED; 即有Euclid性和最大公因式.
$f(x),g(x)\in K[x]$, $g(x)|f(x)\iff r(x)=0$.
$f(x)\in K[x]$, $\forall K[x]$ 上不可约多项式 $p(x)$, ${\rm deg}p\leq {\rm deg}f$, s.t. $p(x)\nmid f(x)$, 则 $f(x)$ 为 $K[x]$ 上不可约多项式.

定理: 域 $F$ 上 $F[x]$, $f(x)\in F(x)$, 则 $F[x]/f(x)$ 为域 $\iff f(x)$ 为 $F[x]$ 上不可约多项式.
特别有素数 $p$ 和 $F[x]$ 上不可约多项式 $degr=n$, $F_p[x]/<r(x)>=\{\sum_{i=0}^{n-1}a_0x^i\ |\ a_i\in F_p\}\cong F_{p^n}$, 即有 $|F_p[x]/<r(x)>|=p^n$.

有限域结构: $\forall$ 素数 $p$, $n\in\mathbb{Z}_+$, 存在同构意义下唯一的有限域 $F_{p^n}$ s.t. $|F_{p^n}|=p^n$, ${\rm char}(F_{p^n})=p$.

• NTRU: 环 $L=\mathbb{Z}[x]/(x^n-1)$, $n$ 为大素数; 选取大数 $p,q$, 有 ${\rm gcd}(p,q)=1$ 且 $q\ll p$; 选取 $f(x),g(x)\in L$, 有 ${\rm deg}f={\rm deg}g=n-1$.
  $f^{-1}_p(x)$ 为 $f(x)$ 系数模 $p$ 逆, $f^{-1}_q(x)$ 为 $f(x)$ 系数模 $q$ 逆; $h(x)\equiv f^{-1}_q(x)({\rm mod}\ q)$.
  公钥 $(n,p,q,h(x))$, 明文多项式 $m(x)=\sum a_ix_i$ 有 $|a_i|\leq \frac{p-1}{2}$ 及 ${\rm deg}m\leq n$, 随机选取噪音 $r(x)\in L$, 加密 $c(x)\equiv pr(x)h(x)+m(x)({\rm mod}\ q)$.
  私钥 $(f(x),f^{-1}_p(x))$, 解密 $d(x)\equiv f(x)c(c)({\rm mod}q)$, $b(x)\equiv d(x)({\rm mod}\ p)$, $m(x)\equiv f^{-1}_p(x)({\rm mod}\ p)$.

椭圆曲线群

定义: 域 $F$, $a,b,c,d,e\in F$, 满足Weierstrass方程 $E=y^2+axy+by=x^3+cx^2+dx+e$ 所有点 $(x,y)$ 和无穷远点 $O$ 的集合.

Hasse定理: 有限域 $GF(p)$ 上椭圆曲线, $n$ 为 $E$ 上点 $(x,y)$, $x,y\in\mathbb{Z}_p$ 的个数, 则 $|n-(p+1)|\leq 2\sqrt p$.

有限域上椭圆曲线: 有限域 $GF(p)$ 上椭圆曲线 $y^2\equiv x^2+ax+b({\rm mod}\ p)$, $a,b,x,y\in GF(P)$, 且满足 $4a^3+27b^2\not\equiv 0({\rm mod}\ p)$ (此时无重根), 记为 $E_p(a,b)$.

构造: $x$ 遍历 $\in\mathbb{Z}_p$, $t_x\equiv x^3+ax+b({\rm mod}\ p)$, $a,b\in GF(p)$; Euler保留所有模 $p$ 二次剩余的 $t_x$, 并求出两根; $t=0$ 时只有一根 $y=0$.

定理: $E_p(a,b)$ 关于点的加法构成Abel群.
无穷远点 $O$ 为单位元, 逆元为关于 $x$ 轴对称点, 横坐标不同的点(相同的只有自身和逆元)相加为连线延长线与曲线交点关于 $x$ 轴的对称点, 相同点相加为该点处切线与曲线交点关于 $x$ 轴的对称点.

不妨设 $P,Q\in E_p(a,b)$, $P,Q\ne O$, $P=(x_1,y_1)$, $Q=(x_2,y_2)$, $R=P+Q=(x_3,y_3)\ne O$.

则 $x_3=\lambda^2-x_1-x_2$, $y_3=\lambda(x_1-x_3)-y_1$, 其中 $\lambda=\frac{y_2-y_1}{x_2-x_1}\ (P\ne Q);\ \frac{3x_1^2+a}{2y_1}\ (P=Q)$.

• ECDH: 椭圆曲线群 $E_p$, $G\in E_p$, $|G|=q$ 为大素数, 任选 $2\leq a,b\leq q-1$.
  公钥 $(p,G)$, 私钥 $x,y$.
  握手: $k_{A\to B}=aG$, $k_{B\to A}=bG$.
  密钥: $k=ak_{B\to A}=bk_{A\to B}=(ab)G$.

• ECEG: 椭圆曲线群 $E_p$, $G\in E_p$, $|G|=q$ 为大素数, 任选 $2\leq d\leq q-1$, $P=dG$.
  公钥 $(P,G,E,n)$, 加密 $C_1=rG$, $C_2=M+rP$, $C=E_{E_p,P,G,r}(M)=\{C_1,C_2\}$, 任选 $2\leq r\leq q-1$.
  私钥 $d$, 解密 $M=D_{E_p,d}(C)=C_2-dC_1$.
  快速倍乘 $P=mG$, $m\in\mathbb{Z}_p$, $G\in\ E_p(a,b)$.

传统算法

素数定理: $\pi(x)$ 为 $\leq x$ 的素数个数, 有 $\lim_{x\to\infty}\frac{\pi(x)}{x/\ln x}=1$.

• Fermat测试: 若 $n$ 为素数, $a\in\mathbb{Z}$, $1\leq a\leq n-1$, 则 $a^{n-1}\equiv 1({\rm mod}\ n)$. 随机测试 $t$ 次, 确为素数可能性大于 $1-\frac{1}{2^t}$.

1
2
3
4
5
6
7

bool fermat(int n){
    int a,r;
    srand((unsigned int)time(0));
    a = rand()%p+1;
    r = fastPowerMod(a,p-1,p);
    return r == 1;
}

• Solovay-Stranssen测试: Jacobi符号 $(\frac{a}{m})=\prod(\frac{a}{p_i})^{\alpha_i}$, 其中 $n=\prod(p_i^{\alpha_i})$. 若 $n$ 为素数, $x=(\frac{a}{n})$, $y\equiv a^{\frac{n-1}{2}}({\rm mod}\ n)$, 则 $x\equiv y({\rm mod}\ n)$.

1
2
3
4
5
6
7
8
9

bool solovayStrassenX(int p){
    int a, x, y;
    srand((unsigned int)time(0));
    a = rand()%p+1;
    x = jacobi(a,p); // jacobi同fastLegendre
    x = (x+p)%p;
    y = fastPowerMod(a,(p-1)/2,p);
    return x != 0 && x == y;
}

• Millar-Rabin测试: Fermat测试时, 不妨设 $a^{n-1}=(a^t)^{2^k}$, $a^t\equiv 1({\rm mod}\ n)$ 则直接满足素性条件, 否则检验 $a^t$ 的 $i=1,…,k-1$ 次平方, $(a^{t})^{2^i}\equiv -1({\rm mod}\ n)$ 时直接满足素性条件.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

bool millerRabin(int p){
    int k = 0, t = p-1, a, r;
    while(t%2 == 0){
        t >>= 1;
        ++k;
    }
    srand((unsigned int)time(0));
    a = rand()%p+1;
    r = fastPowerMod(a,t,p);
    if (r == 1){
        return true;
    } else{
        for (int j = 0; j < k; ++j) {
            if (r == p-1){
                return true;
            } else {
                r = (1LL*r*r)%p;
            }
        }
    }
    return false;
}

大合数分解: 试除法时间复杂度 $O(\sqrt n)$.

• Pollard-$\rho$ 法: 有限集上随机函数存在碰撞; $n$ 不为素数或某个素数的幂, 寻找小因子.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

int rho(int n){
    int a = 2, b = 2, d;
    do {
        a = ((1LL*a*a)+1)%n;
        b = ((1LL*b*b)+1)%n;
        b = ((1LL*b*b)+1)%n;
        d = gcd(a-b,n);
        if ((1 < d) && (d < n)){
            return d;
        }
    } while (d != n);
    return -1;
}

• Pollard-$p-1$ 法: 素数 $p|n$, $p-1$ 分解中素因子最大次幂 $q|p-1$, $\forall B\geq q$ s.t. $p-1|B$, 即 $2^{B!}\equiv 2^{p-1}\equiv 1({\rm mod}\ p)$, 故有 $p|{\rm gcd}(n,2^{B!}-1)$.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

int pollard(int n){
    int B = 24;
    int a = 2;
    for (int i = 2; i <= B; ++i) {
        a = fastPowerMod(a,i,n);
    }
    int d = gcd(a-1,n);
    if ((d > 1) && (d < n)){
        return d;
    }
    return -1;
}

• 随机平方法: $x,y\in\mathbb{Z}$ s.t. $x^2\equiv y^2({\rm mod}\ n)$, $x\not\equiv\pm y({\rm mod}\ n)$, 若 $n|x^2-y^2$ 且 $n\nmid x-y$ ($n\nmid x+y$), 则素数 $p={\rm gcd}(x+y,n)$ ($p={\rm gcd}(x-y,n)$).

离散对数求解: 有限域 $F_p$ 上遍历需要 $O(p)$ 次乘法.

• 小步大步法(Shank): 群阶为 $n$, $m=\lceil\sqrt n\rceil$, 设 $\log_a b=x=mj+i$, $0\leq i,j\leq m-1$, 即 $b(a^{-i})=(a^m)^j$; 搜索树存储 $1,a^m,…,(a^m)^{m-1}$, 遍历 $b(a^{-i})$ 并匹配.

• Pollard-$\rho$ 法: 素数 $p$, $a,b\in\mathbb{Z}_p^*$, 不妨设 $x_i=a^{m_i}b^{n_i}$, 有碰撞 $x_i=x_{2i}$ 时, 有 $\log_a b\equiv (n_{2i}-n_i)^{-1}(m_{2i}-m_i)({\rm mod}\ |a|)$.

$$f(x_{i+1},m_{i+1},n{i_1})=\begin{cases} (bx,m_i,n_i+1),\ & x_i\in S_1 \\ (x^2,2m_i,2n_i),\ & x_i\in S_2 \\ (ax,m_i+1,n_i),\ & x_i\in S_3 \end{cases},\ S_1\sqcup S_2\sqcup S_3=\mathbb{Z}_p^*$$

• 指数演算法: 素数 $p$, 原根 $a\in\mathbb{Z}_p^*$, 小素因子基 $B=\{p_1,p_2,…,p_k\}$, 选取 $k$ 个 $1\leq x\leq p-2$ 均 s.t. $x\equiv \alpha_1\log_a p_1+\alpha_2\log_a p_2+…+\alpha_k\log_a p_k({\rm mod}\ p-1)$, 可解得 $\log_a p_1,\log_a p_2,…,\log_a p_k$; 选取 $1\leq s\leq p-2$ s.t. $\log_a b+s\equiv \gamma_1\log_a p_1+\gamma_2\log_a p_2+…+\gamma_k\log_a p_k({\rm mod}\ p-1)$

• Pohlig-Hellman算法: 素数 $p$, 原根 $a\in\mathbb{Z}_p^*$, 最小原根 $g$, $a\equiv g^m({\rm mod}\ p)$, $b\equiv g^n({\rm mod}\ p)$, 则 $m\log_a b\equiv n({\rm mod}\ p-1)$ 可由扩展Euclid算法给出.
  $p-1=\prod_{i=1}^k p_i^{\alpha_i}$ 中均为小素数, 有 $k$ 个同余式 $m\equiv \sum_{j=0}^{\alpha_i-1} c_{ij}p_i^j({\rm mod}\ p_i^{k_i})$; 由 Fermat 可得 $g^{c_{ij}\frac{p-1}{p_i^{\alpha_i}}}\equiv a^{\frac{p-1}{p_i}^{\alpha_i}}({\rm mod}\ p)$. 遍历并得到 $0\leq c_{ij}\leq p_i^{\alpha_i}-1$; 对 $k$ 个同余式使用CRT即得到 $m$.

古典密码

古典密码主要为置换密码和代换密码.

• 置换密码: $\sigma$ 为 $M$ 上一个置换(到自身的双射).
  加密: $(c_i)=E_{k}((m_i))=\sigma_{k_i}((m_i))$.
  解密: $(m_i)=D_{k}((c-i))=\sigma_{k_i}^{-1}((c_i))$.

• 代换密码
  加密: $c_i=E_{k}(m_i)\equiv f(m_i,k)({\rm mod}\ 26)$.
  解密: $m_i=E_{k}(c_i)\equiv f^{-1}(c_i,k^{-1})({\rm mod}\ 26)$.

单表代换可以直接通过字母频率分析破解.

1
2
3
4
5
6
7
8
9

void freqAnalyze(char *cipher, long *cnt){
    for (long n = 0; cipher[n]; ++n) {
        if (isupper(cipher[n])){
            cnt[cipher[n]-'A']++;
        } else if (islower(cipher[n])){
            cnt[cipher[n]-'a']++;
        }
    }
}

粗糙度: ${\rm M.R}=\sum_{i=0}^{25}(p_i-\frac{1}{26})^2=\sum_{i=0}^25p_i^2-0.0385$. 明文或单表代换时 ${\rm M.R}\approx 0.027$, 更接近 $0$ 则更可能为多表代换.

重合指数: ${\rm IC}=\sum_{i=0}^{25}p_i^2$. 多表代换时 ${\rm IC}\approx 0.0655$. 相同字母间隔为 $d_1,…,d_n$, 则密钥可能长度为 ${\rm gcd}(d_1,…,d_n)$.

自同步序列密码

异或$\rm XOR$ ($GF(2)$加法) $\oplus$ 加密: 无条件安全; 可逆.
与同步序列密码相比, 传输产生的错误有界.

• 种子密钥通过LFSR(线性反馈移位寄存器)生成伪随机密钥序列 $k=k_0k_1k_2…$.
  加密 $c_i=E_{k}(m)=m_i\oplus k_i$.
  解密 $m_i=D_{k}(m)=c_i\oplus k_i$.

LFSR: 状态 $(s_0,s_1,…,s_{n-1})$, 递推关系式 $s_{n+k}=\bigoplus g_is_i$, 反馈函数 $f(s_0,s_1,…,s_{n-1})=\sum g_is_i$, 连接多项式(特征多项式) $g(x)=\sum g_ix_i^i$, $s_i,g_i,x_i\in GF(2)$.

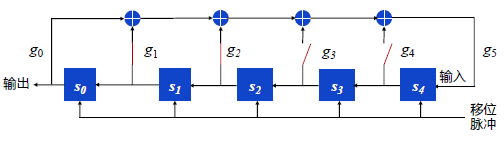
e.g. $\ g(x)=1+x+x^2+x^5$, $s_{5+i}=s_{i}+s_{1+i}+s_{4+i}$.
$S_0=(1,0,1,1,1)$, $k=101110111011101110111…$, $T=8$.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

// 使用verligo实现LFSR.
// 32-bit long
module lfsr(32)(clk, reset, lfsr);
  input clk, reset;
  output reg [31:0] lfsr;
  wire d0;

  xnor(d0, lfsr[31], lfsr[21], lfsr[1], lfsr[0]);

  always @(posedge clk, posedge reset) begin
    if(reset) begin
      lfsr <= 32'h00000001;
    end
    else begin
      lfsr <= {lfsr[30:0], d0};
    end
  end
endmodule

定理: $n$ 次特征多项式为 $GF(2^n)$ 上本原多项式时, 输出 $\max T=2^n-1$ 序列($m$ 序列).
将 $x^{2^n-1}-1$ 在 $GF(2^n)$ 上因式分解;
保留次数为 $n$ 且不能在 $GF(2^n)$ 上整除 $x^a-1,n<a<2^n-1$ 的因式.

截获长度 $l\geq 2(2^n-1)$ 的明密文对 $(c,m)$, 则 $k=c\oplus m$, 有状态 $S_i,…,S_{i+n+1}$;
记 $X=(S_i,…,S_n)$, $Y=(S_{i+1},…,S_{i+n+1})$, 有 $Y\equiv HX({\rm mod}\ 2)$.
$m$ 序列时, $X$满秩, $H\equiv YX^{-1}({\rm mod}\ 2)$ 为特征多项式的友矩阵.

$$H=\left( \begin{array}{} 0 & 1 & 0 & … & 0 \\ 0 & 0 & 1 & … & 0 \\ … \\ 0 & 0 & 0 & … & 1 \\ g_0 & g_1 & g_2 & … & g_{n-1} \end{array}\right )$$

可引入非线性运算增加复杂性: 与AND($GF(2)$上乘法) $\otimes$.

RC4

基于非线性数据表变换. 密钥流产生分为2个阶段:
(1) 输入密钥并初始化排列S表;
(2) S表不断置换产生密钥流.

• 初始化: 线性填充256字节S表, 密钥循环填充T表. $i$ 遍历 $0-255$, $j=(j+S[i]+T[i])\%256$, 交换 $S[i]$ 和 $S[j]$.

• 产生密钥流: $i$ 循环遍历 $0-255$, $j=(j+S[i])\%256$, 交换 $S[i]$ 和 $S[j]$, $t=(S[i]+S[j])\%256$, $k_i=S[t]$.

安全问题: 存在弱密钥使得初始化置换后 $S$ 表顺序不变; 存在弱密钥使得密钥流在100万字节内完全重复; 密钥较短的容易被攻击, 但长度超过128位的密钥依然有效.

ZUC

LTE-4G国际标准, 包含机密性128-EEA3和完整性128-EIA3, 基于LFSR的非线性组合逻辑结构.
分为三层结构: LSFR, Bit重组, 非线性F函数.
符号约定: $\boxplus$ 为$GF(2^{32})$ 上加法; $|$ 为连接字符串; $_H$ 为高位16位; $_L$ 为低位16位; $< <_o$ 为循环左移.

• 输入参数: COUNT 计数器 32bit; BEARER 传载层标识 5bit; DIRECTION 传输方向标志 1bit; CK 密钥 128bit; IBS 输入比特流(明文或密文).

• 密钥装入: 128bit扩展为16个31bit, $k=k_0|k_1|…|k_{15}$, $v=v_0|v_1|…|v_{15}$; 其中 $iv_0={\rm COUNT}[0]$, $iv_1={\rm COUNT}[1]$, $iv_2={\rm COUNT}[2]$, $iv_3={\rm COUNT}[3]$, $iv_4={\rm BEARER}|{\rm DIRECTION}|00$, $iv_5=iv_6=iv_7=00000000$, $iv_{j+8}=iv_j$, $j=8,9,…,15$.

• LSFR: 连接多项式为 $GF(2^{31}-1)$ 上本原多项式 $g(x)=x^{16}-2^{15}x^{15}-2^{17}x^{13}-2^{21}x^{10}-2^{20}x^{4}-2^8-1$; 输出 $m$ 序列周期 $T=(2^{31}-1)^{16}-1$; 生成16个31bit LFSR块.

• Bit重组: $X_0=S[15]_H|S[14]_L$, $X_1=S[11]_L|S[9]_H$ ,$X_2=S[7]_L|S[5]_H$, $X_3=S[2]_L|S[0]_H$.

• 非线性F函数: $W=(X_0\oplus R_1)\boxplus R_2$, $W_1=R_1\boxplus X_1$, $W_2=R_2\boxplus X_2$, $R_1=S(L_1(W_{1L}|W_{2H}))$, $R_2=S(L_2(W_{2L}|W_{1H}))$; 其中 $L_1(a)=a\oplus(a< <_o 2)\oplus(a< <_o 10)\oplus(a< <_o 18)\oplus(a< <_o 24)$, $L_2(a)=a\oplus(a< <_o 8)\oplus(a< <_o 14)\oplus(a< <_o 22)\oplus(a< <_o 30)$; $S$ 盒为 $(S_0,S_1,S_0,S_1)$, 每8bit作为索引, 返回 $S$ 盒中对应的8bit数值.

• 密钥流输出: $K=W\oplus X[3]$, 每个时钟节拍产生32bit密钥流.

• 输出参数: OBS 输出比特流(密文或明文).

ZUC生成密钥流分为5个阶段:
(1) $ck$ 和 $iv$ 装载到LFSR;
(2) 寄存器 $R_1,R_2$ 置空;
(3) 初始化模式运行32次;
(4) 工作模式运行1次并舍弃输出;
(5) 持续工作模式产生密钥流.

安全问题: 能够抵御多种已知针对序列密码的攻击, 主要威胁是侧信道攻击.

分组密码

本质为单表代换, 复杂多轮非线性, 通过混淆和扩散实现.
组件: S盒(混淆扩散), P置换(扩散), 轮函数F, 密钥扩展.

• 结构模型
  S-P网络: 每轮异或密钥后, S盒分组小块混淆扩散, P置换整体扩散, $N_i=F(N_{i-1}\oplus K_i)$.
  Feistel网络: 分为左右两部分, $R_i=F(R_{i-1},K_i)\oplus L_{i-1}$, $L_i=R_{i-1}$, 最后一轮不做对换; 同个算法实现加解密.

• 工作模式:
  ECB(电子密码本): 分组用相同密钥加密; 相同明文产生相同密文; 可并行.
  CBC(密码分组链接): 初始化 $iv$ 得到第一组密文, 第一组密文与第二组明文异或后再加密; TSL及IPSEc协议推荐; 仅解密支持并行.
  CFB(密文反馈): 初始化 $iv$ 得到密文 $E$, $vi$ 左移 $n$ 位, 密文 $E$ 与明文异或后得到密文 $C$, $C$ 高位 $n$ 位填入 $vi$; 流式数据, 错误有界; 仅解密支持并行.
  OFB(输出反馈): 初始化 $iv$ 得到密文 $E$, $vi$ 左移 $n$ 位, 密文 $E$ 与高位 $n$ 位填入 $vi$, 密文 $E$ 与明文异或后得到密文 $C$; 流式数据, 错误有界; 不支持并行.
  CTR(计数器): 自增算子加密后与明文异或得到密文; 相当于一次一密; 简单快速安全可并行.
  

DES

数据加密标准(Data Encryption Standard), 体现Shannon密码设计思想, 公开密码算法先例, 16轮Feistel网络对合加解密.

• 密钥扩展: 初始密钥(64bit)经PC1表置换得到 $C_i$ 和 $D_i$ (各28bit), 循环左移 $ls_i$ 位, 经PC2表置换得到第 $i$ 轮子密钥 $K_i$ (48bit); 置换表中元素 $pt_{i}$ 意为将待置换中的第 $pt_{i}$ 位置换到第$i$位.

• 初始置换与结束逆置换: 明(密)文(64bit)经IP表置换进入加密, 完成加(解)密后经IPR表置换得到密(明)文(64bit).

• 轮函数: 32bit输入经E表置换扩充到48bit, 与子密钥(48bit)异或后, 经S盒压缩回32bit(混淆), 再经P表置换得到32bit输出(扩散); S盒6位输入 $b_1b_2b_3b_4b_5b_6$, 输出$s_{b_1b_6, b_2b_3b_4b_5}$.

S盒是DES中唯一非线性变换, 设计准则: 改变1bit输入至少2bit发生变化; $S(x)$ 和 $S(x\oplus 001100)$ 至少2bit发生变化; $S(x)\neq S(x\oplus 11ef00)$, $e,f\in{0,1}$; 改变5bit输入, 输出的0和1数目大致相等; 足够的非线性度以抵抗线性攻击; 差分性均匀以抵抗差分攻击; 足够的代数次数和项目以抵抗插值攻击和高阶差分攻击.

攻击类型: 穷钥攻击; 侧信道攻击(能量分析, 故障注入分析); 差分攻击; 线性攻击.

安全问题: 密钥太短(有效仅56bit); 存在弱密钥; 互补对称性(异或运算).

3-DES: 112(1和3轮密钥相同)/256bit密钥; 加解密速度慢.

AES

高级数据加密标准(Advanced Encryption Standard), 采用10/12/14轮S-P网络非对合加解密(对应128/192/256bit密钥).

$GF(2)$ 上多项式域 $GF(2^8)\cong GF(2)[x]/(x^8+x^4+x^3+x+1)$ 中元素为 $b_{(8)}=b_7x^7+b_6x^6+b_5x^5+b_4x^4+b_3x^3+b_2x^2+b_1x+b_0$, 乘法需对既约多项式 $m(x)=x^8+x^4+x^3+x+1$ 取模, 乘法逆元可由扩展Euclid算法得到.
考虑 $xb_{(8)}=(b_{(8)}< < 1)\oplus m(x)$, 高次乘法可重复 $x$ 乘实现.

$GF(2^8)$ 上 $degf\leq 3$ 多项式环 $GF(2^8)/[x^4+1]$ 中元素为 $b_{(32)}=B_3x^3+B_2x^2+B_1x+B_0$, 乘法需对 $x^4+1$ 取模. 考虑 $xb_{(32)}=b_{(32)}> >8$, 高次乘法可视为 $GF(2^8)$ 上矩阵乘法.

• 状态矩阵: 128bit明(密)文和密钥按列优先载入4阶方阵, 每列32bit称为"字", 加(解)密后按列优先输出密(明)文.

• 密钥扩展: 4字输入, 扩展为44字输出; $w[i]=w[i-1]\oplus w[i-4]$, $i\% 4 \ne 0$; $w[i]=w[i-4]\oplus S(w’[i-1])\oplus Rcon[i]$, $i \% 4 = 0$, 即每个字循环左移1字节后进行S盒置换.

• 轮函数: 主要包括(逆)字节代换, (逆)行位移, (逆)列混合, 轮密钥加(即子密钥异或).

字节代换即取求每个字节在 $GF(2^8)$ 上的逆后进行仿射变换, 可等效为S盒置换; 逆字节代换即逆仿射变换再取逆, 可等效为逆S盒置换.
行位移即第 $i=0,1,2,3$ 个字循环右移 $i$ 字节; 逆行位移即第 $i$ 个字循环左移 $i$ 字节.
列混合即按列的字在 $GF(2^8)[x^4+1]$ 上与 $a(x)={\rm 0x03}x^3+{\rm 0x01}x^2+{\rm 0x01}x+{\rm 0x02}$ 相乘; 逆列混合即与 $a^{-1}(x)={\rm 0x0B}x^3+{\rm 0x0D}x^2+{\rm 0x09}x+{\rm 0x0E}$ 相乘; 均可等效为 $GF(2^8)$ 上的矩阵乘法.

安全问题: 主要威胁是侧信道攻击.

SM4

128bit密钥32轮非平衡Feistel网络. 1字$=$4字节$=$32bit.

• 密钥扩展: 初始密钥 $(MK_0,MK_1,MK_2,MK_3)$, $K_i=MK_i\oplus FK_i$ ,$rk_i = K_{i+4} = K_i\oplus T(K_{i+1}\oplus K_{i+2}\oplus K_{i+3}\oplus CK_i)$; $FK_i$ 为系统参数, $CK_i$ 为固定参数; 以每个字节前4bit作为行, 后4bit作为列, 进行非线性的S盒置换; 再对字进行线性变换 $B\oplus (B < <_o 13)\oplus (B < <_o 23)$.

• 轮函数: $X_{i+4} = X_i\oplus T’(X_{i+1}\oplus X_{i+2}\oplus X_{i+3}\oplus rK_i)$; S盒8位输入 $b_1b_2b_3b_4b_5b_6b_7b_8$ 输出$s_{b_1b_2b_3b_4, b_5b_6b_7b_8}$, 再对字进行线性变换 $B\oplus (B < <_o 2)\oplus (B < <_o 10)\oplus (B < <_o 18)\oplus (B < <_o 24)$.

• 反序输出: 输入 $(X_1,X_2,X_3,X_4)$, 输出 $(Y_1,Y_2,Y_3,Y_4)=(X_{35},X_{34},X_{33},X_{32})$.

安全问题: 主要威胁是侧信道攻击(故障注入分析).

公钥密码

使用对称加密, $n$ 个实体的网络需要 $\frac{(n-1)n}{2}$ 个密钥及同等数量的保密信道, 密钥管理困难.
对称加密也难以解决签名和认证问题: 接收方可以伪造原文; 发送方可以否认行为.

非对称加密基本条件: (1)安全 $k_e\ne k_d$ 且由 $k_e$ 不能得到 $k_d$; (2) 保密: $D(E(m))=m$; (3)E和D高效; (4) 保真: $E(D(m))=m$.

单向陷门函数: $y=f(x)$ 满足: (1)给定 $x$, 计算 $y$ 很容易; (2)给定$y$, 不掌握陷门, 计算 $x=f^{-1}(y)$ 很困难; (3)给定$y$, 掌握陷门, 计算 $xf^{-1}(y)$ 很容易.

• 数学难题
  大合数分解难题: 大素数乘积容易 $p\times q=n$, 大合数分解困难 $n=p\times q$.
  离散对数难题(DLP): 有限域 $GF(p)$ 上生成元幂乘容易 $a^b=c$, 求对数困难 $\log_a c=b$.
  椭圆曲线离散对数难题(ECDLP): 椭圆曲线群 $E_p(a,b)$ 中基点倍乘容易 $dP=Q$, 求倍数困难 $d=\frac{Q}{P}$.
  误差还原难题(LWE): 有限域 $GF(p)$ 上矩阵乘法加误差容易 $v=As+e$, 解带噪音的线性方程组困难 $s=A^{-1}(v-e)$.
  

• 工作方式
  发送方 $A$: 先用发送方私钥 $k_{Ad}$ 签名 $s=D(m,k_{Ad})$, 再用接收方公钥 $k_{Be}$ 加密 $c=E(s,k_{Be})$.
  接收方 $B$: 先用接收方私钥 $k_{Bd}$ 解密 $s=E(c,k_{Bd})$, 再用发送方公钥 $k_{Ae}$ 验证 $m=D(s,k_{Ae})$.
  机密性: 公钥加密, 私钥解密.
  真实性: 私钥签名, 公钥验证.
  

RSA

• RSA: 素数$p,q$, $n=pq$, ${\rm gcd}(e,\varphi(n))=1$, $\varphi(n)=(p-1)(q-1)$.
  公钥 $(e,n)$, 加密 $c=E_{e,n}(m)\equiv m^e({\rm mod}\ n)$.
  私钥$d\equiv e^{-1}({\rm mod}\ \varphi(n))$, 解密 $m=D_{d,n}(m)\equiv m^d({\rm mod}\ n)$
  

证明: $D_{d,n}(E_{e,n}(m))=m$, $E_{e,n}(D_{d,n}(c))=c$.

即证 $m_{ed}\equiv m^{(t\varphi(n))+1} \equiv m({\rm mod}\ n)$.

${\rm gcd}(M,n)=1$ 时, 有Euler定理 $m^{\varphi(m)}\equiv 1({\rm mod}\ n)$.

${\rm gcd}(M,n)\ne 1$ 时, 由于 $m\leq n$, 不妨设 $m = ap$, $a\in\mathbb{Z}$, 有 $m^{\varphi(q)}\equiv 1({\rm mod}\ q)$, 即 $m^t{\varphi(n)}=bq+1$, $b\in\mathbb{Z}$, 故 $m^t{\varphi(n)+1} = abn+M$.

• 参数选取
  $p,q$ 足够大, 一般场景使 $n$ 达到1024bit, 重要场景2048bit.
  $p,q$ 为强素数, $p-1,p+1,q-1,q+1$ 中均无除 $2$ 外的小因子.
  $p,q$ 位数不能相差过大或过小.
  私钥 $d\ne e$.
  ${\rm gcd}(p-1,q-1)$ 尽可能小, 最好为2; 以避免密文迭代攻击.
  $e$ 应保证 $m^e\ll n$; 有人建议为素数 $2^{16}+1=65537$, 二进制表示中仅含两位 $1$, 加密速度较快.
  $d$ 应较小以保证解密速度, 但确保$d\ll \frac{n}{4}$.
  多个用户不得共用同一个模 $n$; 以避免共模攻击.

• 大素数产生: Miller-Rabin测试.

• 加密优化算法: 快速模幂, Montgomery.

• 解密优化算法: CRT, 快速模幂, Montgomery.

Montgomery: $a\%m=a-k\times\lfloor[\frac{a}{m}]\rfloor$ 除法运算复杂度较高, 将模乘转换为乘法运算.
记 $a’\equiv aR({\rm mod}\ m)$, $b’\equiv bR({\rm mod}\ m)$, $R=2^k>m$, $m$ 为奇数, 即 ${\rm gcd}(R,m)=1$; 此时 $a’R^{-1}=a’> >k$, $abR\equiv (a’b’)R^{-1}({\rm mod}\ m)$, $ab\equiv (abR)^R{-1}({\rm mod}\ m)$.
$\exists q$ s.t. $R|a+qm$, 有 $y=\frac{a+qm}{R}<2m$; 不妨设 $xR-ym=1$, $0<y<R$, $0<x<m$, 有 $q\equiv ay({\rm mod}\ R)$, 其中 $y\equiv -m^{-1}({\rm mod}\ R)$.

ElGamal型

• D-H协议: 大素数 $p$ 和模 $p$ 原根 $g$, 任选 $2\leq x,y\leq p-2$.
  公钥 $(p,g)$, 私钥 $x,y$.
  握手: $k_{X\to Y}\equiv g^x({\rm mod}\ p)$, $k_{Y\to X}\equiv g^y({\rm mod}\ p)$.
  密钥: $k\equiv k_{Y\to X}^x\equiv k_{X\to Y}^y \equiv g^{xy}({\rm mod}\ p)$.
  

• ECDH: 椭圆曲线群 $E_p$, $G\in E_p$, $|G|=q$ 为大素数, 任选 $2\leq a,b\leq q-2$.
  公钥 $(p,G)$, 私钥 $x,y$.
  握手: $k_{A\to B}=aG$, $k_{B\to A}=bG$. 密钥: $k=ak_{B\to A}=bk_{A\to B}=(ab)G$.

• ElGamal: 大素数 $p$ 和模 $p$ 原根 $g$, 任选 $2\leq a\leq p-2$, $Y_a\equiv g^a({\rm mod}\ p)$.
  公钥 $(p,g,Y_a)$, 加密 $u\equiv g^k({\rm mod}\ p)$, $v\equiv mY_a^k({\rm mod}\ p)$, $c=E_{p,g,Y_a,k}(m)=(u,v)$, 任选 $2\leq k\leq p-2$, $k\ne a$.
  私钥 $a$, 解密 $m\equiv D_a(c)\equiv \frac{v}{u^a}({\rm mod}\ p)$.
  参数选取: $p$ 足够大, 一般场景512bit, 重要场景1024bit.

• ECEG: 椭圆曲线群 $E_p$, $G\in E_p$, $|G|=q$ 为大素数, 任选 $2\leq d\leq q-2$, $P=dG$.
  公钥 $(P,G,E,q)$, 加密 $C_1=rG$, $C_2=M+rP$, $c=E_{E_p,P,G,r}(M)=\{C_1,C_2\}$, 任选 $2\leq r\leq q-2$, $r\ne d$.
  私钥 $d$, 解密 $M=D_{E_p,d}(C)=C_2-dC_1$.
  参数选取: $p$ 足够大, 一般为160bit; 余因子 $h=\frac{|E_p|}{|G|}\leq 4$; 避免选用超奇异和反常椭圆曲线.

SM2

SM2本质为ECEG.

• 初始化: 椭圆曲线群 $E_p$, $G\in E_p$, $|G|=q$ 为大素数, 任选 $2\leq d\leq q-2$, $P=dG$, $h=\frac{|E_p|}{|G|}\leq 4$.
  避免选取非超奇异和反常椭圆曲线, $p$ 达到 160bit, $h\leq 4$, $S=hP\neq O$.
  公钥 $(P,G,E,q)$, 私钥 $d$.
  

• 加密: 生成 $2\leq r\leq q-1$, $r\ne d$, $(x_1,y_1)=rG$, $(x_2,y_2)=rP$, $t=k(x_2 || y_2)$.
  密钥派生函数 $k$: 32bit计数器 ${\rm ct}={\rm 0x01}$, 得到 $\lfloor\frac{{\rm len}}{v}\rfloor$ 个hash值 $h=H(x_2 || y_2 || {\rm ct})$, 并截断为 ${\rm len}$; 其中 ${\rm len}$ 为 $m$ 长度, $v$ 为hash值长度, 一般采用SM3.
  $C_1=x_1 || y_1$, $C_2=m\oplus t$, $C_3=h(x_2 || m || y_2)$, $c=C_1 || C_2 || C_3$

• 解密: $(x_2,y_2)=dC_1$, $t=k(x_2 || y_2)$, $m=C_2\oplus t$; $u=H(x_2 || m || y_2)$, 验证 $u=C_3$.

Hash函数

Hash/杂凑/散列: 将任意长度消息变为固定长度的信息摘要/数字指纹/Hash值/杂凑值/散列值, 记 $h=H(m)$.

单向性(抗原像攻击): 给定 $h$, 找到 $m’$ 有 $h(m’)=h$ 在计算上不可行.
抗弱碰撞性(抗第二原像攻击): 给定 $m$, 找到另一 $m’$ 有 $H(m)=H(m’)$ 在计算上不可行.
抗强碰撞性: 找到一对 $(m,m’)$ 有 $H(m)=H(m’)$ 在计算上不可行.
随机性: 输出具有伪随机性.
有效性: 运算高效.
错误检测: 输入发生很小变化都会使得输出很大不同.

应用: 完整性保护; 消息认证码(MAC); 辅助公钥加密, 数字签名, 密钥交换.

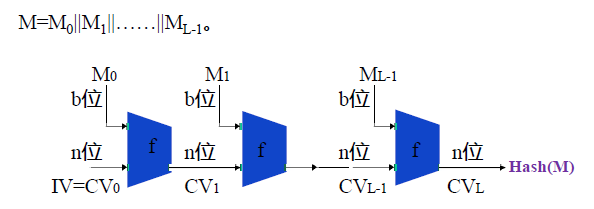
消息填充: 加密分组为 $l$ bit, 最后 $m$ bit 存放消息长度, 将原消息填充到 $s$ bit, 有 $l|s+m$.
迭代型结构(Merkle-Damgard): 每轮 $l$ bit和上一轮输出一同加密得到下一轮输出.

MD5

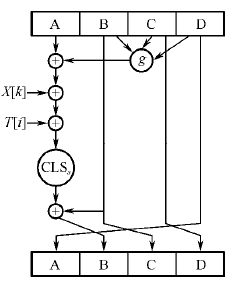
Message-Digest Algorithm(消息摘要算法).

消息填充后(长度以小端序存储), 以512bit分组, 每轮对4个寄存器各1word(32bit)进行16轮迭代, 最后得到128bit输出.

SHA-256

Secure Hash Algorithm(安全Hash算法).

消息填充后(长度以大端序存储), 以512bit分组, 每组扩展为64word(2048bit), 每轮对8个寄存器各1word(32bit)进行64轮迭代, 最后得到256bit(8word)输出.

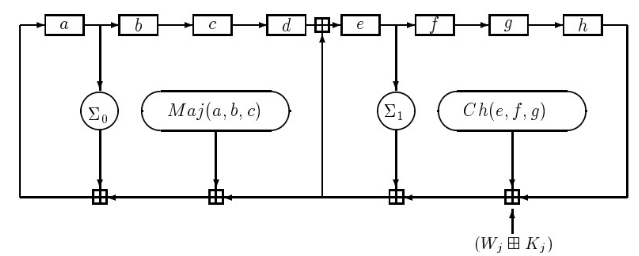
SM3

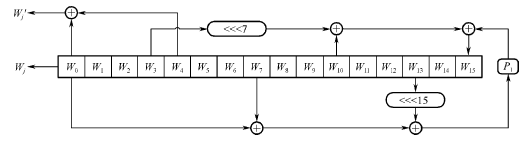
消息填充后(长度以大端序存储), 以512bit分组, 每组扩展为132word(4224bit), 每轮对8个寄存器各1word(32bit)进行64轮迭代, 最后得到256bit(8word)输出.

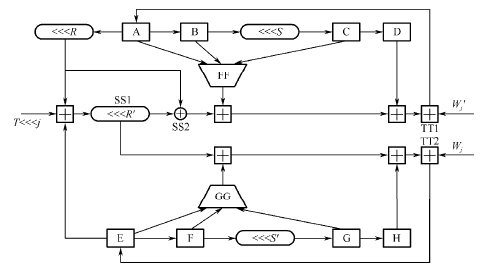
HMAC

Message Authentication Code(消息认证码/密码校验和): 验证消息真实性
共享密钥 $k$, 发送方发送 $({\rm MAC}=C_k(m),m)$, 接收方比较 $C_k(m’)={\rm MAC}’$.

HMAC: 基于Hash函数的MAC.
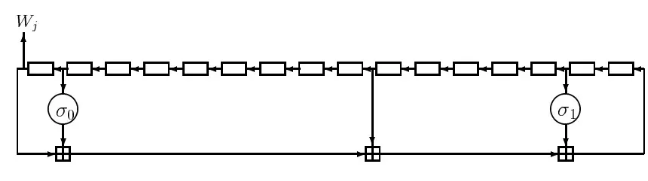
${\rm HMAC}_k=H[(k^+\oplus {\rm opad}) || H[(k^+\oplus {\rm ipad}) || M]]$
Hash分组大小为 $l$ bit$: k^+$ 为左侧填充0至 $l$ bit; ${\rm opad}$ 为 01011010 循环填充到 $l$ bit; ${\rm ipad}$ 为 00110110 循环填充到 $l$ bit.

数字签名

数字签名: 验证消息真实性和身份合法性.
特点: 签名与文件绑定; 不可抵赖性; 不可伪造性; 第三方可验证性.
发送方签名 $\delta={\rm sgn}(m,k_d)$, 接收方比较 ${\rm vrf}(m’,k_e)=\delta’$.

RSA签名

• RSA: 素数$p,q$, $n=pq$, ${\rm gcd}(e,\varphi(n))=1$, $\varphi(n)=(p-1)(q-1)$.
  私钥 $d\equiv e^{-1}({\rm mod}\ \varphi(n))$, 签名 $\delta={\rm sgn}(m,d)\equiv m^d({\rm mod}\ n)$.
  公钥 $e$, 验证 $m’={\rm vrf}(m’,e)\equiv \delta^e({\rm mod}\ n)$.

安全性: 依赖于大整数因子分解
共模伪造: $\delta_1\equiv m_1^d({\rm mod}\ n)$, $\delta_2\equiv m_2^d({\rm mod}\ n)$, 可得 $\delta_1\delta_2\equiv (m_1m_2)^d({\rm mod}\ n)$.
中间人攻击: 加密信息 $c\equiv m^e({\rm mod}\ n)$, 伪造信息 $c’\equiv r^em^e({\rm mod}\ n)$, 签名 $(c’)^d\equiv rm({\rm mod}\ n)$, 造成 $m$ 泄漏.
一般不对消息直接签名, 而对消息的hash值签名; 加密密钥对和签名密钥对分离; 先签名再加密.

现实: 加密 RSA-OAEP; 签名 RSA-PSS/PLCS.

ElGamal型签名

• ElGamal: 大素数 $p$, 有循环群 $F_p^*=\langle g\rangle$.
  私钥 $2\leq x\leq p-2$, 签名 $(m,\delta=(r,s))$, 其中 $r\equiv g^k({\rm mod}\ p)$, $s\equiv k^{-1}(m-rx)({\rm mod}\ p-1)$, 选取 $2\leq k\leq p-2$ 且 ${\rm gcd}(k,p-1)=1$.
  公钥 $y\equiv g^x({\rm mod}\ p)$, 验证 $g^m\equiv r^sy^r({\rm mod}\ p)$.

安全性: 依赖于(EC)DLP
$k$ 一次性, 否则联立 $\delta_1 \equiv k^{-1}(m_1-rx)({\rm mod}\ p-1)$ 和 $\delta_1 \equiv k^{-1}(m_2-rx)({\rm mod}\ p-1)$, 造成私钥 $x$ 泄漏.

• DSA: 大素数 $p$ 且大素因子 $q|p-1$, $q$ 至少160bit, 生成元 $g\equiv h^{\frac{p-1}{q}}({\rm mod}\ p)>1$, 即 $|g|=q$.
  私钥 $2\leq x\leq p-2$, 签名 $(m,\delat=(r,s))$, 其中 $r\equiv (g^k({\rm mod}\ p))({\rm mod}\ q)$, $s=k^{-1}(H(m)+rx)({\rm mod}\ q)$, 选取 $2\leq k\leq q-2$.
  公钥 $y=g^x({\rm mod}\ p)$, 验证 $r\equiv g^uy^v({\rm mod}\ q)$, 其中 $u\equiv H(m)s^{-1}({\rm mod}\ q)$, $v\equiv rs^{-1}({\rm mod}\ q)$.

• ECDSA: 椭圆曲线群 $E_p(a,b)$, 基点 $|G|=n$, 余因子 $h=\frac{|E_p|}{p}$.
  私钥 $2\leq d\leq n-2$, 签名 $(m,\delta=(r,s))$, 其中 $kG=(x_1,y_1)$, $r\equiv x_1({\rm mod}\ n)$, $s\equiv k^{-1}(H(m)+rd)({\rm mod}\ n)$, 选取 $2\leq k\leq n-2$.
  公钥 $P=dG$, 验证 $r\equiv x_2({\rm mod}\ n)$, 其中 $u\equiv H(m)s^{-1}({\rm mod}\ n)$, $v\equiv rs^{-1}({\rm mod}\ n)$, $uG+vP=(x_2,y_2)$.

SM2签名

在SM2加密算法的基础上, 本质为ECEG.

• 初始化: 椭圆曲线群 $E_p$, $G\in E_p$, $|G|=q$ 为大素数, 任选 $2\leq d\leq q-2$, $P=dG$, $h=\frac{|E_p|}{|G|}\leq 4$.
  选取非超奇异和反常椭圆曲线, $p$ 达到 160bit, $h\leq 4$, $S=hP\neq O$.
  公钥 $(P,G,E,q)$, 私钥 $d$.
  

• 签名: $(m,\delta=(r,s))$, 其中 $kG=(x_1,y_1)$, $r\equiv H(Z||M)+x_1({\rm mod}\ q)$ 且 $r\ne 0$ 及 $r+k\ne q$, $s\equiv (1+d)^{-1}(k-rd)({\rm mod}\ q)$ 且 $s\ne 0$, 选取 $2\leq k\leq q-2$.

• 验证: $r+s\not\equiv 0({\rm mod}\ q)$ 且 $r\equiv x_2({\rm mod}\ q)$, 其中 $sG+(r+s)P=(x_2, y_2)$.

身份认证

• 口令
  安全问题: 弱口令易被暴力破解和字典攻击; 口令明文传输和明文保存易导致泄漏.
  解决办法: 口令加盐Hash存储; 通过TSL传输.

• 挑战-应答
  实现方案: 数字签名.
  安全问题: 依赖于密钥管理; 需确保用户公钥的真实性和完整性以避免中间人攻击.

• ZKP(零知识证明): 使验证者(V)确信证明者(P)能够证明某一信息, 但无法获得其他任何信息.

• 基于DLP的认证协议: P向V证明知道私钥 $x$, 而不泄露 $x$; $p$ 为大素数, 公钥 $y\equiv g^x({\rm mod}\ p)$.
  承诺: P随机选取 $2\leq k\leq p-2$ 并发送 $r\equiv g^k({\rm mod}\ p)$.
  挑战: V随机发送 $b\in{0,1}$.
  应答: P发送 ${\rm sgn}\equiv k+bx({\rm mod}\ p-1)$.
  验证: V验证 $g^s\equiv ry^b({\rm mod}\ p)$.
  重复 $t$ 次, P欺骗成功概率为 $\frac{1}{2^t}$.

• Schnorr协议: P向V证明知道私钥 $x$, 而不泄露 $x$; $p$ 为大素数, 大素数 $q|p-q$, $g$ 为模 $q$ 原根, 公钥 $y\equiv g^x({\rm mod}\ p)$.
  承诺: P随机选取 $2\leq k\leq q-2$ 并发送 $r\equiv g^k({\rm mod}\ p)$.
  挑战: V随机发送 $1\leq e\leq 2^t<q$.
  应答: P发送 $s\equiv k-ex({\rm mod}\ q)$.
  验证: V验证 $r\equiv g^sy^e({\rm mod}\ p)$.
  无需重复, P欺骗成功概率为 $\frac{1}{2^t}$.